"Top N out of XDY > CV"
The most traditional way to employ dice rolls in games is in the form XdY > CV , where X is the number of dice in the pool, Y is the number of sides on each dice, and CV is the challenge value.
Implied in this notation is the idea that we're supposed to add up the values rolled in the dice pool before comparing them with the challenge value.
But there is another way! My eyes were opened by Grant Howitt's Sexy Battle Wizards, though in discussions with rpg people I've learned this idea was already floating about in the RPG aether. It's very simple: Instead of adding up the values in the pool, compare each individual roll to the CV! This opens up a whole new style of dice game. Mixed-dice pools are suddenly much more interesting. Counting the number of dice which beat the CV is an awesome way to mete out varying degrees of success!. You can also apply the opposite test: How many dice in the pool fall below a given minimum value! Very exciting possibilies.
I asked the nice people over at r/RPGdesign about a good notation for this mechanic, and several good ones were suggested, including:
1@XdY > CV, the anydice.com notation.XdYk1 > CV, k1 for "Keep 1". Andmax(XdY) > CV, which doesn't allow for 'keeping' more than the top dice, but is perhaps the most self-explanatory of the bunch.
Anyways, I wrote a little code to study of this system, and below I share my results with you in glorious color-coded table format:
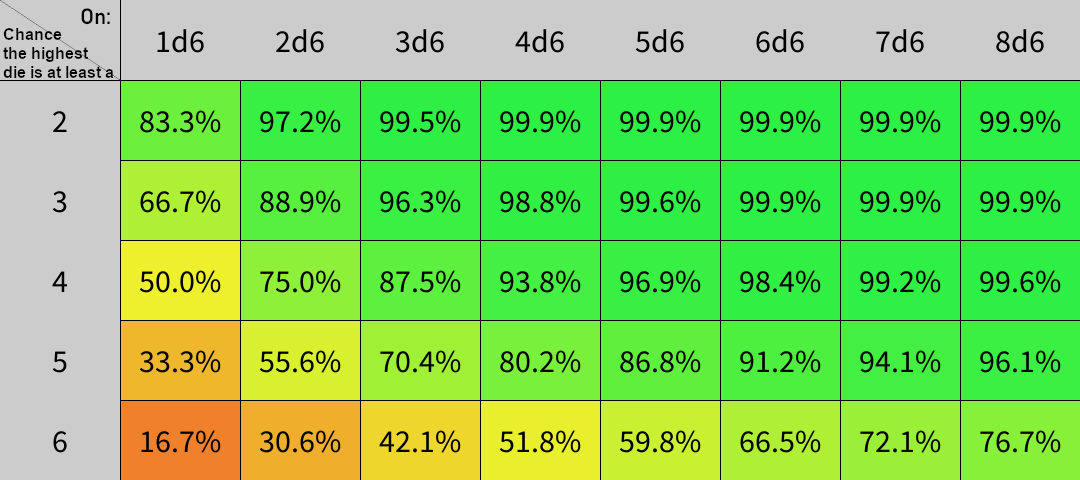
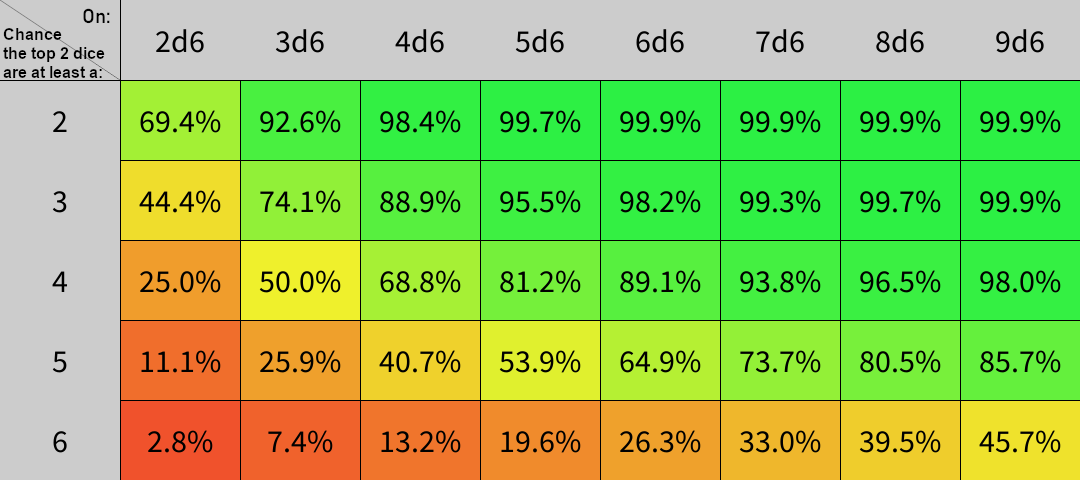
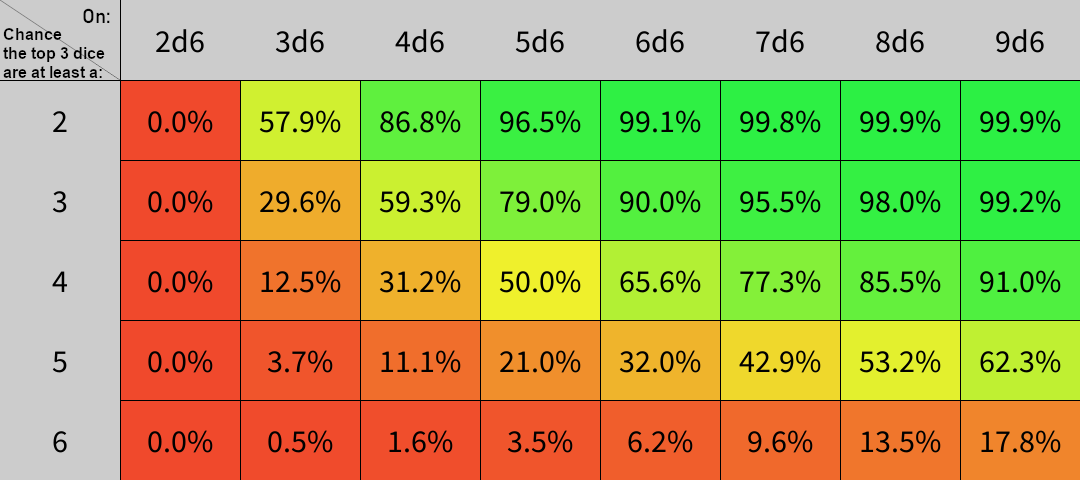
Here's the code!
"Dice Poker"
Poker can be generalized as a very simple game of applying patterns to a list of randomly generated values. The deck of cards is one of the most popular analog random-number-generation system in our culture. The other one is... Dice! Cards are analogous to the faces of dice, rolling dice is analogous to drawing a card. There are somewhat popular "poker dice" out there, but they are really not necessary to implement a simple poker-like dice game. You probably worked all this out by yourself anyways, so let's get on to the tables:

Obviously I've made a lot of decisions here about what kinds of patterns I'm considering "hands". I felt 6d6 was a solid basis for a game of dice poker, and went from there. The progression of values as you add more dice is surprising in some cases, but I don't have the statistics chops to make sense of it. If you do, let me know!
You may have noticed the rows add up to way more than 100%, so yes, the values you see here do indeed count overlapping hands. I whipped up a handy venn diagram to check the 6d6 row:
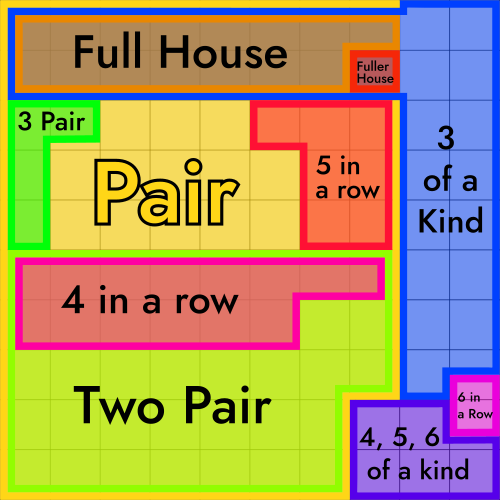
Lots of rounding errors but it does the job. Also the 'fuller house' zone is supposed to overlap the '4 of a kind'. Forgive me. The 'pure pair' space in the middle should be about ~11%, I went back and counted them separately.
Based on these stats, we can derive the following scoring schema:
| Hand | frequency/6 | SCORE |
|---|---|---|
| six of a kind | 1 | 3000 |
| five of a kind | 30 | 100 |
| two trios | 50 | 60 |
| fuller house | 75 | 40 |
| six in a row | 120 | 25 |
| three pair | 300 | 10 |
| four of a kind | 375 | 8 |
| five in a row | 600 | 5 |
| four in a row | 1080 | 2.77778 |
| full house | 1200 | 2.5 |
| three of a kind | 2450 | 1.22449 |
| two pair | 3000 | 1 |
| pair | 6075 | 0.493827 |
| Hand | frequency | SCORE |
|---|---|---|
| six of a kind | 216 | 583.333 |
| five of a kind | 3150 | 40 |
| two trios | 8400 | 15 |
| fuller house | 12600 | 10 |
| six in a row | 15120 | 8.33333 |
| three pair | 26250 | 4.8 |
| four of a kind | 33600 | 3.75 |
| five in a row | 37800 | 3.33333 |
| four in a row | 42000 | 3 |
| full house | 88200 | 1.42857 |
| three of a kind | 122850 | 1.02564 |
| two pair | 126000 | 1 |
| pair | 229950 | 0.547945 |
Scores are = (two-pair frequency) / (hand frequency).
So close to being all integers! Shame. I thought about suggesting some multiple that gives the least amount of rounding error, but I figure that exercise is best left to the reader, after all, different projects will have vastly different requirements when it comes to the figures. You may want to slap a log scale on them, for instance. That 3000 points for the six-of-a-kind is mighty spiky, though it is fair.